
Demo that it should be possible to calculate a 4-D transform such as used by OpenGL to produce an elliptical gradient with arbitrary center point.
A 4-D transform is a 4x4 matrix. It is multiplied by the vector x,y,0,1 to produce the values X*W,Y*W,z*W,W. Dividing the first 2 by the last W value produces the output X,Y.
This example is just distorting an image, producing artifacts due to the input pixels and due to the algorithim being unprepared for such extreme distortions. In the actual implementation the matrix would be inverted and used to produce an input x,y. sqrt(x*x+y*y) would produce the index into the gradient map. This inverted matrix can be calculated directly from the ellipse and center point information without too much difficulty. Transforms of the pattern can be achieved by multiplying the matrix by another matrix, so that the resulting shading calculation is exactly the same speed.
Here is the source image. This is best thought of as a 2x2 square centered on the origin. The circle has a radius of 1:

This shows that a 4-D transform still produces a circle, but the center point can be moved (if you can turn off the visibility of the red channel you can see just the circle and not be distracted by the perspective of the rectangle):
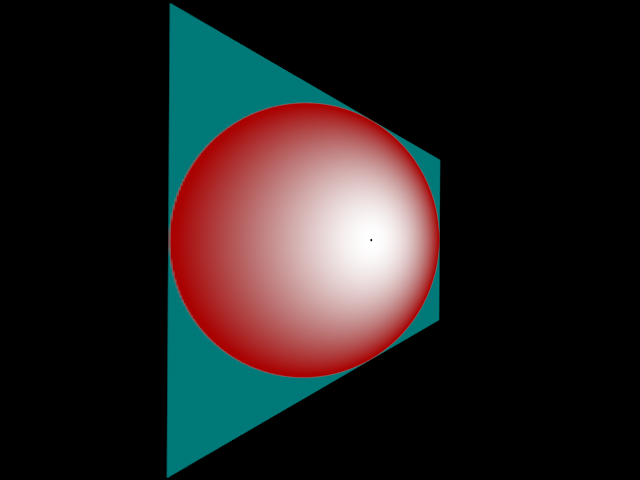
This shows that with more extreme transformations the center can be moved quite close to the edge without making it not be a circle. In the actual implementation the output image would be smooth since it is directly calculated, not looked up from an image:

Example showing a more typical ellipse with slight offset of the center, and that rotations of the ellipse axis are also gotten from this:
